Теоретико-множественные операции#

Пересечение#

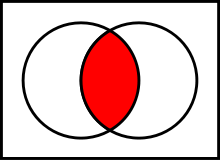
Пересечением множеств A и B называется множество, обозначаемое как \(A \cap B\) и состоящее из тех и только тех элементов, которые принадлежат к множеству A и B одновременно.

\(A \cap B = \{\mspace{5mu} x \mspace{5mu} | \mspace{5mu} (x \in A) \wedge (x \in B) \mspace{5mu} \}\)

Объединение#

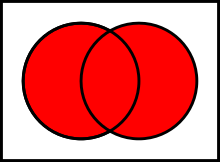
Объединением множеств A и B называется множество, обозначаемое как \(A \cup B\) и состоящее из тех элементов, которые принадлежат хотя бы к одному из множеств A или B.

\(A \cup B = \{\mspace{5mu} x \mspace{5mu} | \mspace{5mu} (x \in A) \lor (x \in B) \mspace{5mu} \}\)

Теоретико-множественная разность#

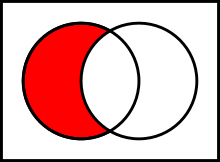
Теоретико-множественной разностью множеств A и B называется множество, обозначаемое как \(A \setminus B\) и состоящее из тех и только тех элементов, которые принадлежат множеству A и не принадлежат множеству B.

\(A \setminus B = \{\mspace{5mu} x \mspace{5mu} | \mspace{5mu} (x \in A) \wedge \neg (x \in B) \mspace{5mu} \}\)

Над статьей работали:

• Лавелин Михаил (Тг): редактор

Выражаем благодарность:

• Олегу Вадимовичу, за конспект для данной статьи